How will quantum computing help us in the search for new pharmaceuticals?
You may have heard that quantum computers are going to change the world and that the breakthroughs will include new battery technology as well as faster drug discovery.
At the end of last year I took you through some of the ideas you need to understand Shor’s algorithm for factorizing large numbers. This algorithm gets a lot of press because if we can factorize large numbers then everything we do from banking to social media will no longer be secure. We are a little way off having quantum computers powerful enough to do that because you need quite a lot of qubits to factorize any interestingly large number.
Instead, the first really useful quantum computers will focus on much more quantum-y problems where the quantum computer has a much larger architectural advantage. Those will be areas in which we are currently using classical computers to simulate quantum behaviour. Classical computers are not well placed to simulate quantum systems. Even with the largest supercomputers it is very expensive to simulate systems with just a few molecules. By contrast, with relatively few qubits it is possible to determine molecule properties quickly, dramatically speeding up drug discovery and other areas of computational chemistry.
What do I need to understand in order to follow this blog?
Applications of quantum computing in computational chemistry require a little background on quantum computing and quantum mechanics. In this post I will assume that you have a reasonable understanding of the topics covered in previous posts, in particular:
- Quantum Chemistry: Understanding the Schrödinger Equation
- A mini guide to Eigenfunctions
- Preparing the Hamiltonian matrix for quantum computing algorithms
You by no means have to digested every aspect of the articles above, but if you don’t know what it means to find the eigenfunctions of the Hamiltonian to solve the Schrödinger equation then I would start with those blogs before going much further here. If you are really new to quantum computing then you may also want to check out Quantum computing: a nerdy introduction and the articles linked from there.
How do quantum computers do computational chemistry?
Two commonly deployed algorithms for computation chemistry in quantum computing are Quantum Phase Estimation (QPE) and the
Variational Quantum Eigensolver (VQE). We met QPE when we were looking at Shor’s algorithm. It was used to find the phase of the unitary operator used to calculate xᵃ mod N. More generally, QPE can be used to find that phase of any unitary operator. It is used in computational chemistry to find the energy levels of a given system.
VQE is different in that it is a hybrid approach using both classical and quantum computing. This hybrid approach means that it is a likely candidate for early practical application of a quantum computer. It doesn’t need as many qubits as other quantum algorithms and the quantum circuit is not as deep as in other algorithms. VQE is used to find the ground state of a given molecular system. The ground state is the lowest possible energy of a system.
Why do energy levels matter?
The energy levels of a molecular system tell us its properties. For example, the energy levels tell us how reactive two substances are, or whether it will conduct electricity. Remember that quantum systems can have only discrete energy levels. In drug discovery, knowing the energy levels of a system will tell us how likely a drug is to bind to a protein and how stable that reaction will be. It will tell us how quickly a drug will be metabolized. We can even theorize about how a drug will diffuse through the blood or whether it will be able to pass through a cell membrane. To understand the energy levels of the system we need know both the ground states of that system as well as the energy levels of excited states.
Why is it hard to calculate energy levels for a system?
To find the energy levels of the system you solve the Schrödinger equation to find the wave form of the quantum system.

To solve the Schrödinger equation you define the system in terms of a Hamiltonian operator then find the eigenfunctions of the Hamiltonian, which define the waveform and also the eigenvalues, which are the possible energy levels of the system.
One can define the Hamiltonian for a given system, but as you include, for example, the position and spin of each electron, the effect each electron has on each other electron, the position, energy levels and charge distributions of the nucleus, it gets more complicated. Then you need to add in some effects from quantum field theory and relativity and scale up to not just one atom, but to large complex molecules that are interacting. It is still possible to solve but the complexity has moved past what one can do on paper and pencil and to an equation that would take a long time to solve on a supercomputer.
Applying the Variational Quantum Eigensolver to the problem
The VQE algorithm can be used for a various optimization problems in chemistry and machine learning, but here we are going to look at how you use it to find an estimate for the energy ground state of a system.
To apply VQE you need to define the Hamiltonian for the system. You also need to define a trial wavefunction. This is a guess for the wave function. VQE exploits the condition that given the Hamiltonian H-hat and wave function Ψ, the expectation value must be larger than or equal to the lowest eigenvalue, the energy ground state.

The expectation value of a Hamiltonian and wave function is the average or mean energy of the wave function and is calculated as above. The goal of VQE is to try values of the wave function that minimize the expectation value in order to estimate the ground state.
To allow the wave function to be varied it must be in some way parameterized. More parameters give a larger search space and so increase the likelihood of finding a good approximation for the ground state, but more parameters also increases the computational complexity and therefore the cost of running the algorithm. The parameterized wave function forms an approximation for the eigenfunction corresponding to the eigenvalue that is the ground state.
VQE is a hybrid quantum algorithm meaning that you use both a classical computer and then you use a quantum computer. The quantum computer is used to evaluate the expectation value of that wave function and the Hamiltonian. This evaluation is often called the cost function. The classical compute part uses an optimizer to minimize the expectation value by varying the parameters of the wave function.
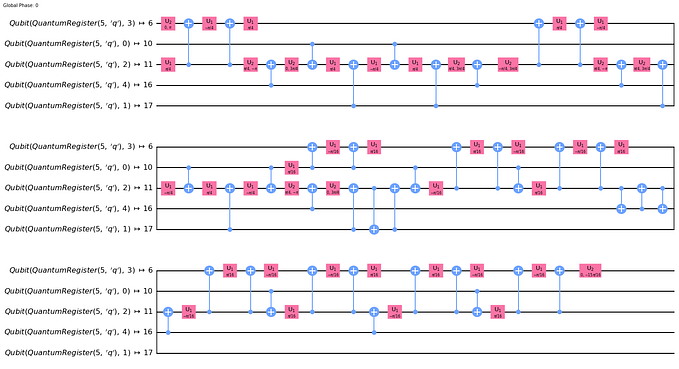
The diagram below shows a high level description of the quantum circuit of VQE. The first part of the circuit prepares the parameterized wave form. The second part of the circuit measures the expectation value of the wave form given an encoded Hamiltonian for the system. This expectation value is fed back to the classical optimizer and the parameters of the wave form are updated.

Defining and encoding the Hamiltonian
The first step in VQE is to define the molecular system in terms of a Hamiltonian that can be presented on a quantum computer. To build the Hamiltonian you define the kinetic energy which is the energy of the particles in isolation, and you define the energy of any possible interactions. Usually this starts from a representation of the position of each atom and electron in space and the terms are built from there, taking into account the affect each particle will have on the next. Unfortunately the Hamiltonian in that form is not usable by a quantum algorithm. To apply the VQE or similar quantum algorithms, the Hamiltonian must be simplified, defined as a matrix using a basis set of quantum states, and then encoded using gates that can be implemented on a quantum computer. This is a complex topic all of its own so I’ve outlined some of the theory behind this in another post, but I include a summary here in the context of the VQE algorithm.
To represent the Hamiltonian in a useful way it is first simplified, often using second quantization, and then it is encoded using gates that can be implemented on the quantum computer. Second quantization exploits the idea that identical particles in the same state are interchangeable. Encoding the Hamiltonian into quantum computing gates is easier when it is represented in first quantization, but there are methods for mapping from second quantization representations of the Hamiltonian.
Defining the Hamiltonian as a matrix that can be mapped to quantum computing gates involves choosing a basis. A basis is a set of functions that can be used to build the wave function. A common choice is a set of atomic orbitals. The basis choice defines the number of qubits needed to simulate the Hamiltonian and it also affects the complexity of the circuit and the accuracy of the results so it is an important part of the algorithm implementation.

Usually the Hamiltonian is encoded on the quantum computer as a linear combination of Pauli strings. Pauli strings are tensor products of Pauli gates, which are single qubit gates that can be implemented on a quantum computer. Representation of the Hamiltonian in this way allows evaluation of the expectation value of the wave form and Hamiltonian on a quantum computer, which is the quantum cost function of the VQE.
Preparing the ansatz wave function
The ansatz or trail wave function is also critical to the efficiency and precision of the algorithm. It is common to choose a waveform that can remain unchanged throughout the full run of the algorithm. The quantum circuit that prepares the wave form can therefore remain unchanged. The wave form is varied between successive iterations via a parameter set so the quantum circuit that prepares the qubits with the wave form must be parameterizable.
Both the choice of ansatz and the set of parameters must be expressive enough to be able to find the ground state with reasonable accuracy, however not be so expressive that the search space is too large. An ansatz with many parameters will cover a larger space which is more likely to include a good approximation for the ground state, but it will be more computationally expensive.
A problem that is common to many optimization algorithms such as VQE is that of the barren plateau where the gradient is so flat it is not possible to optimize. If the gradient is smaller than the measurement precision then the optimizer can get stuck in a random walk around the plateau. A poor choice of ansatz with flat areas will therefore increase runtime and make it more expensive to compute the ground state.
There are many methods proposed for choosing the ansatz, each with advantages and disadvantages. Some methods yield an ansatz that is more resilient against the barren plateau problem and all of them trade off trainability and expressibility. Some ansatz are also hardware specific, exploiting specific aspects of the quantum computer implementation.
A common way to construct the ansatz is a method called the Hardware Efficient Ansatz. It does not contain physical or chemical information about the system and as such has a number of flaws or drawbacks where physical affects in the system are not accounted for, but it is built directly using quantum gates so is straightforward and efficient to construct. It consists of layers of rotations and entanglement operators.

The rotations are rotations of the bloch sphere in the x, y or z axis and are parameterized via the angle θ of rotation:
Rₓ = eⁱᶿˣ
Although the Hardware Efficient Ansatz misses some of the details of a real system, with careful application is represents an efficient way to approximate the wavefunction in order to find the ground state of the Hamiltonian with the desired precision.
Measurement of expectation values
Once the wave form has been constructed, the expectation value of the waveform and Hamiltonian must be calculated. The expectation value is the mean energy level. To measure the mean value the circuit must be run multiple times and the mean value calculated. To extract increasing precision from the cost function the circuit must be run increasing numbers of times. The number of iterations needed depends on the level of precision needed, but it does not depend on the size of the system to be modeled so does not affect the complexity of the algorithm.
Each iteration of the quantum circuit is called a shot. Each term in the Hamiltonian encoding requires a set of shots, with the number of shots required increasing with the precision required. Some terms in the encoding of the Hamiltonian can be combined to reduce the number of shots required so the design of the encoding strategy it important. In particular, Pauli strings that commute, that is Pauli strings that can be applied in one order or the other with the same result, can be combined into one operation. We need to minimize the number of shots as we aim for quantum advantage.
Measuring the expectation value for each term in the Hamiltonian encoding can be done in a number of different ways. One approach is the Hadamard test. Note that in the context of the Hadamard test the H denotes a Hadamard gate, not the Hamiltonian operator.
Selecting the classical optimizer
Once the quantum circuit has been designed for both the Hamiltonian and the waveform, the classical part of the algorithm must be developed. Often a gradient optimizer is used where the gradient of the expectation value is calculated in addition to the expectation value at a given point, in order to inform the next set of parameters to try. There is also a more specialized technique called the Rotosolve which has been specifically designed as an optimizer for VQE. This algorithm exploits the fact that the trial waveform is composed of rotations around the bloch sphere. It is likely I think that as quantum computing advances and we get closer to practical application of VQE on large molecular system then additional optimizers will be developed that exploit emerging trade offs in precision and performance between the evolving quantum and classical computers.
Error mitigation and error correction
VQE has been designed for the NISQ era, where NISQ stands for Noisy Intermediate-scale Quantum. It is error tolerant by design because it uses fewer qubits and shallower circuits than other similar algorithms, but still requires more qubits and a greater depth of circuit than is possible today. Quantum error correction is also likely to be a key part in achieving practical application of VQE alongside careful selection of the encoding of the problem.
Bringing it all together
VQE has attracted a lot of attention because it requires fewer qubits and a shallower circuit than other algorithms for finding energy levels and ground states. The ansatz and representation of the Hamiltonian can be designed such that they scale with polynomial complexity thus exhibiting an advantage over a purely classical approach.
The algorithm does however require a lot of expert tuning and there are many ways in which the algorithm can drop in efficiency. Perhaps as quantum computers advance and we start to apply these techniques in anger some clear winners will emerge. Hopefully at that point developer toolkits will start to make it easier to bring together a set of choices that work reliably for this algorithm.
I hope that you have enjoyed learning about this algorithm. A much deeper understanding is needed for real application of these techniques, but my goal was to leave you with an intuition about what quantum algorithms look like and how they are used. None of us can be sure when algorithms like VQE will be viable, but I believe they will be within my lifetime. I am looking forward to the advances in medicine and clean energy technology that will hopefully come from this revolution.